Inari Listenmaa

Fixpoints in gftest, part II
Welcome to part II! This won’t make any sense without reading part I so do that if you didn’t already.
Workflow in gftest
This is a short summary of how gftest works—you can read our paper or my thesis if you want more details. The following is enough to understand this post.
- Choose a GF function
f : A → B - In PMCFG, it is actually several functions
f¹:A¹→B¹…fⁿ:Aⁿ→Bⁿ - For each concrete function, we generate (best!) arguments
a¹…aⁿ, of typesA¹…Aⁿrespectively, and apply eachfⁱto the corresponding argument. (Read my thesis to find out the definition of best.) - For each subtree
f¹a¹…fⁿaⁿof typesB¹…Bⁿ, generate a set of contexts, which together use all fields from the subtree.
A context for some category C is a tree in the start category, with
a hole of type C. Let’s take the function Mod : Quality → Kind
→ Kind from the
Foods grammar.
In step 3, we supply arguments of types Quality and Kind, such as
Vegan and Pizza, to obtain Mod Vegan Pizza. In step 4, we would
generate a context such as Pred (This _) Good, which we then fill
with vegan pizza: “this vegan pizza is good”.
A string’s journey to the start category
For a given category C, we would like to find paths between it and the
start category. To be more precise, just enough different paths that
all of its string fields get used at least once.
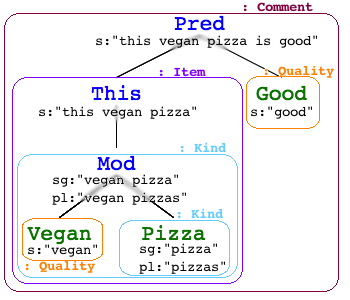
How does a subtree get to show around the strings in its fields? They
need to end up in the s field of a tree in the start category!
If the subtree is the whole tree, then it needs nothing from anyone else to accomplish its goal. “I don’t need any context, I am my own context!” it boasts to its subtrees.
If the subtree is any other tree in a non-start category, then it
depends on other categories in order to make it to the start
category. The s field of Comment is the goal for all categories:
we need to find a succession of function applications that take a
string from some field in C, through all other intermediate
categories, so that it finally ends up in the s field of Comment.
The word depend is a bit counter-intuitive here: normally you’d think that
Item depends on Kind, because the only way to form an Item is
using one of the functions of type Kind → Item. But when we think
of contexts, we say instead that the context of Kind depends on the
context of Item.
Look at Mod Vegan Pizza in the picture: it has two strings that it
would love to show around. But Pred, which is the only function that
creates something in the start category, doesn’t take Kinds. So it
has to rely on This to lift it up into an Item, and only then can Pred get
access to the strings that originally came from Vegan and
Pizza1.
The same story but with more fixpoints
Now let’s stop imagining that syntax trees have feelings and desires2. What do we need to turn this into a fixpoint computation?
The strongest clue was the notion of dependence: in order to compute
contexts for Kind, we need to already have computed contexts for
Item. All categories depend on other categories, except for the
start category.
So, in the beginning we know the optimal path (“do nothing, you’re already there!”) for the start category, but not for other categories. This is a hint that we could do top-down, just like we did when computing reachable categories. Let’s start writing and figure out the actual values and types as we go.
Remember again that contexts are trees with holes, or in other
words, functions of type Tree → Tree. To construct paths, we apply the
trees that are closer to the start category to the trees that are
lower. Well, technically we cannot apply Tree → Tree into another
Tree → Tree–we just get a composition that is still Tree → Tree. But eventually
there will be a Tree: one of those examples we’ve generated at the
step before context generation.
Here is an artist’s illustration on the process:

So what kind of a trivial Tree → Tree function we could use for
Comment? Well, you can’t get more trivial than id : a → a.
CtxComment := { id }
CtxItem := { }
CtxQuality := { }
CtxKind := { }
We also have information on the original grammar: for every category we know which functions take it as an argument, and how manyeth argument it is. In addition, we know which fields from its argument it uses (i.e. sends upwards).
This is just a trivial lookup table we get directly from the
grammar. The notation is as follows: Category ➡ (Function, arg. position, [fields from the argument the function uses]).
Item ➡ (Pred,0,[s]) -- Pred : Item → Quality → Comment
Quality ➡ (Pred,1,[s])
,(Mod,0,[s]) -- Mod : Quality → Kind → Kind
Kind ➡ (This,0,[sg]) -- This,That,… : Kind → Item
,(That,0,[sg])
,(These,0,[pl])
,(These,0,[pl])
,(Mod,1,[sg,pl])
Round 1
With this information, can we now find some contexts for Item?
CtxComment := { id }
CtxItem := { ctx (Pred • 🐰) | ctx ← CtxComment }
CtxQuality := { }
CtxKind := { }
Looks promising! By the way, remember that ctx comes from
CtxComment, which only contains id. So CtxItem reduces
to {Pred • 🐰}.
Where did that 🐰 come from? Just take it as a placeholder: “we’re
going to need something else here too, but let’s not worry about it
now–the string we pick from Item is not affected by it. So keep
calm, here’s a rabbit.”
And that dot •? That’s where the Item is going to go.
In fact, on this same round we get a first context for Quality as
well!
-- Round 1 finished
CtxComment := { id }
CtxItem := { ctx (Pred • 🐰) | ctx ← CtxComment }
CtxQuality := { ctx (Pred 🐰 •) | ctx ← CtxComment }
CtxKind := { }
The first context comes from the same function, Pred. The only
difference is that Pred takes Quality as its second argument; so
now we place the rabbit as a placeholder for the first argument.
Note that for Item, Pred was the only function that ever takes it
as an argument. For Quality, we have another option (Mod), but we
cannot unlock it yet, because Mod returns a Kind, and we haven’t
unlocked any contexts for Kind yet!
Round 2
As we go on the second round, we will compute a context for
Kind. Let’s have our first try:
CtxComment := { id }
CtxItem := { ctx (Pred • 🐰) | ctx ← CtxComment }
CtxQuality := { ctx (Pred 🐰 •) | ctx ← CtxComment }
CtxKind := { ctx (That •) | ctx ← CtxItem }
Okay, now we’re running into trouble. For the first time, we have a
choice of 4 Kind → Item functions. I just picked one that was
alphabetically the first and hoped we get something type-correct.
In fact, there’s a missing piece of information in the context lists: we also need to store the fields that make it to the top! So let’s add that information into the contexts we have so far:
CtxComment := { ( id , [s] ) }
CtxItem := { ( ctx (Pred • 🐰), [s] )
| (ctx,_) ← CtxComment }
CtxQuality := { ( ctx (Pred 🐰 •), [s] )
| (ctx,_) ← CtxComment }
CtxKind := { ( ctx (That •) , [sg] )
| (ctx,_) ← CtxItem }
This shows more clearly that we’re not done yet: we only cover the
sg field, but all Kinds have also a pl field. This could be a
possible step in the fixpoint computation–maybe the contexts from
categories that are so far unlocked don’t have anything that uses pl
field. But we actually know it’s not true: there are functions
that use the pl field, we just didn’t know how to pick them.
Let’s make the computation for CtxKind more general:
CtxKind := { ( ctx (F •) , fields used by F )
| (ctx,_) ← CtxItem
, F ← functions of type Kind → Item }
Now this is better, but slightly redundant: we end up with more
contexts than we need. Thus we add a pruning step, which adds a new
context for C only if it covers fields not yet in CtxC. (More
details later.) Since all of This, That, These, Those just
cover one field, we probably end up picking the alphabetically first
variants, That and These. Now let’s finally look at our
contexts!
-- Round 2 finished
CtxComment := { ( id , [s] ) }
CtxItem := { ( ctx (Pred • 🐰), [s] )
| (ctx,_) ← CtxComment }
CtxQuality := { ( ctx (Pred 🐰 •), [s] )
| (ctx,_) ← CtxComment }
CtxKind := { ( ctx (That •) , [sg] )
, ( ctx (These •) , [pl] )
| (ctx,_) ← CtxItem }
In fact, we are done, even without consulting all functions! That’s
the benefit of going top-down: we don’t waste time trying out
functions that may lead anywhere. Consider Quality for instance:
we’d eventually found our way to Comment even by following Mod
first, but why bother when Pred already takes a Quality directly
to Comment?
In English, we don’t bother, because there’s only one field in
Quality. Now let’s take a hypothetical language that is just like
English, except that adjectives come in two variants, attributive and
predicative.
LangEng> the warm pizza is warm
LangDut> de warme pizza is warm
Actually it exists and is called Dutch. Now we’ve got two fields for
Quality–let’s call them pred and attr. The function Pred
covers the field pred, and we need to wait until the 3rd round,
when CtxKind is no more empty, to find a context that covers attr.
Round 3 (Dutch only)
CtxComment := { ( id , [s] ) }
CtxItem := { ( ctx (Pred • 🐰), [s] )
| (ctx,_) ← CtxComment }
CtxQuality := { ( ctx (Pred 🐰 •), [pred] )
| (ctx,_) ← CtxComment } ∪
{ ( ctx (Mod • 🐰) , [attr] )
| (ctx,_) ← CtxKind }
CtxKind := { ( ctx (That •) , [sg] )
, ( ctx (These •) , [pl] )
| (ctx,_) ← CtxItem }
And now we’re done for Dutch as well. Before we go on de-bunnifying the contexts, let’s talk about the pruning step in a bit more detail.
Important points on pruning
For fixpoint purposes, it’s important that we implement the pruning
function in a way that prioritises the already computed contexts,
because otherwise we’d be throwing away old and replacing them with
new all the time, and the sets would not converge. It would go like
“oh cool, this Mod Vegan (Mod Good (Mod Warm (Mod Green •))) sure is
a totally new and exciting context, better throw away the Mod Good
(Mod Warm (Mod Green •)) that already covered the same fields”. Nope,
we keep the first one that covers sg, first one that covers pl,
and so on.
Well there’s a small exception: assume that we added a whole new
abstract syntax construction of type Kind → Item, which uses both
singular and plural in one sentence!
Then we get just one context which covers [sg,pl], and thus we throw
away both (ctx (That •), [sg]) and (ctx (These •), [pl]), in
favour of, say, (ctx (ThisAndThese •), [sg,pl]).
So, the set of contexts for a category C may change during the
fixpoint computation. It grows as we unlock contexts for more
categories, further down from the start category. It may also shrink,
if we find a single context that covers the fields from multiple,
previously computed, contexts. But most importantly, the list of
fields from C that make it into the start category is growing
throughout the fixpoint computation. It’s just the way those fields
are clumped into contexts that changes.
Apply and de-bunnify the contexts
Let’s go back to English, and finish the context business. Here’s a reminder of what we got from the fixpoint computation.
CtxComment := { ( id , [s] ) }
CtxItem := { ( ctx (Pred • 🐰), [s] )
| (ctx,_) ← CtxComment }
CtxQuality := { ( ctx (Pred 🐰 •), [s] )
| (ctx,_) ← CtxComment }
CtxKind := { ( ctx (That •) , [sg] )
, ( ctx (These •) , [pl] )
| (ctx,_) ← CtxItem }
This table contains the contexts for all categories! Let’s try them out one by one.
Okay let’s do Kind, because it doesn’t have the bunnies. The
variable ctx comes from CtxItem, so let’s evaluate that first.
CtxKind := { ( ctx (That •) , [sg] )
, ( ctx (These •) , [pl] )
| (ctx,_) ← { ctx' (Pred • 🐰)
| (ctx',_) ← CtxComment} }
Help, nested set comprehensions! Let’s reduce a bit:
CtxKind := { ( ctx' (Pred (That •) 🐰) , [sg] )
, ( ctx' (Pred (These •) 🐰) , [pl] )
| (ctx',_) ← CtxComment }
Looks better. Let’s keep reducing those expressions, we’re almost done
(CtxComment only contains id).
CtxKind := { ( Pred (That •) 🐰 , [sg] )
, ( Pred (These •) 🐰 , [pl] ) }
Now these looks like proper contexts! Well, except for the bunnies. So now we get rid of them in a simple step: generate an arbitrary (minimal) subtree of the category whose placeholder the bunny is. That’s it. If you want to be fancy, choose a subtree that has no identical elements to the rest of the context, so we don’t get sentences like “the pizza gives the pizza the pizza”.
The end
That’s all. Now we know how to see context generation as a fixpoint computation.
Footnotes
1. Actually, Pizza is not quite
satisfied–it lost its plural field along the way. So the following is
more like how Pizza would like it. ↩
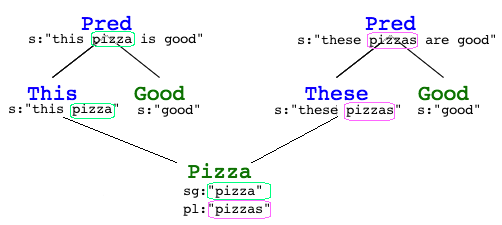
2. If, on the other hand, you liked that, here’s one more illustration just for you! ↩