Inari Listenmaa

Logo

CV · Blog · GitHub

5 December 2018

String, Int and Float literals in GF, part I

Grammar

Here’s a simple grammar that parses expressions such as the following:

abstract Numbers = {
flags startcat = Command ;
cat
  Command ;
fun
  Call    : Int -> Command ;
  Follow  : String -> Int -> Command ;
  Measure : Float -> Command ;
}

With the following concrete syntax in English:

concrete NumbersEng of Numbers = open
  Prelude,
  SymbolicEng,
  SyntaxEng,
  ParadigmsEng in {

lincat
  Command = Imp ;

lin
  Call i =
    mkImp (mkV2 "call") (symb i);
  Follow s i =
    mkImp (mkV2 "follow") (dashNP (symb s) (symb i)) ;
  Measure f =
    mkImp (mkV2 "measure") (symb f) ;

oper
  dashNP : NP -> NP -> NP = \np1,np2 -> np1 **
    {s = \\c => np1.s ! c ++ "-" ++ np2.s ! c} ;
}

Let’s break this down to smaller pieces.

Literals as abstract syntax categories

Look at the abstract syntax. In cat, I have only defined Command, but in fun I’m using the types Int, String and Float. These types are built in GF, and you can see their specification in here.

They are present in all grammars, even if you don’t write them. If you type pg in your GF shell, you’d see something like the following:

cats

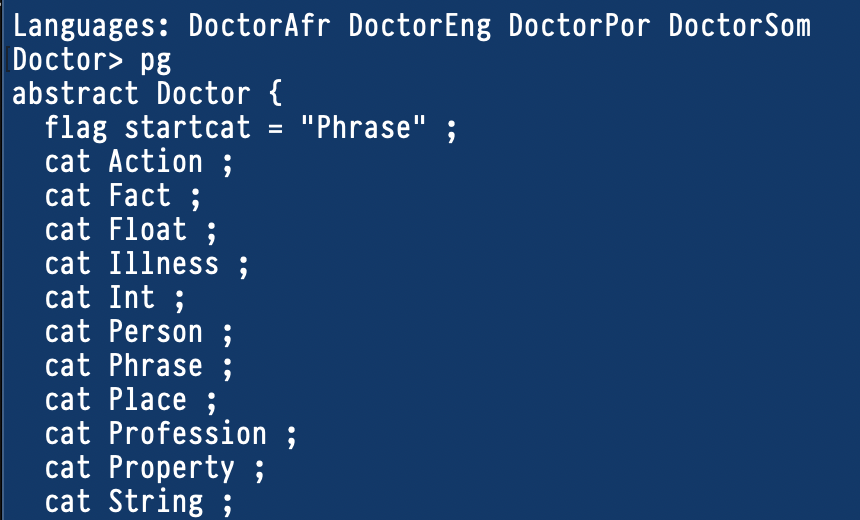
symb and friends

In order to become an object of a verb such as “call” or “measure”, the literal needs to be turned into a GF category like NP. The module Symbolic has an overloaded function symb, which does just that. Check out the link (and the new fancy version of RGL source browser!) to see the API.

In the grammar, I can simply use the function symb that turns an Int into an NP as follows:

lin
  Call i =              -- : NP
    mkImp (mkV2 "call") (symb i) ;

Parsing and linearisation

Parsing works just as expected:

Numbers> p "follow ABC - 123"
Follow "ABC" 123
Numbers> p "call 911"
Call 911

(With the grammar I pasted, you get spaces the registration plate; use BIND to get rid of it.)

You can also linearise any tree you want to (up to integer overflow):

Numbers> l Call 99999999999999
call 99999999999999
Numbers> l Call 9999999999999999999999999999999999
call 4003012203950112767

Generation

If you type gt in e.g. Foods grammar, you get a long and repetitive list of trees like “this very very very Italian wine is very Italian”, and at some point it stops, depending on the --depth parameter.

Generating trees with literals works differently. For both random and exhaustive generation in the GF shell, you only get one of each:

Numbers> gt -cat=Int
999
Numbers> gt -cat=String
"Foo"
Numbers> gt -cat=Float
3.14

This happens in every category that uses literals, so here’s all that gt does for the whole grammar:

Numbers> gt
Call 999
Follow "Foo" 999
Measure 3.14

String vs. Str

In the RGL synopsis, you see functions that take a Str as an argument. For instance, the Str -> Num instance of mkNum, which takes an argument like “35” (in digits) and returns “thirty-five” spelled out. Would it then be possible to transform a literal (Int, Float or String) using such a RGL function?

The answer is no.

What does mkNum : Str -> Num have to do to map “35” to “thirty-five”? It has to pattern-match the string “35”, otherwise it won’t know which numeral to output.

It’s perfectly fine to use an oper like mkNum : Str -> Num when you’re constructing lexicon. By lexicon, I mean any functions (fun in the abstract syntax) that don’t take arguments. As long as the function creates some string from scratch, it can do anything it wants to that string: pattern match, split and concat other strings with +.

But all of these functions, like Call : Int -> Command, take an argument. When a function takes an argument, we can manipulate the argument (literal or not) in much more limited ways. So in this case, you may only take the literal’s string value unchanged—you can’t even look at it!—and construct a few limited categories out of it. That’s what symb does.

(For a longer explanation on when you can or cannot pattern match and glue tokens, see the gotchas post.)

Part II

Part II of this post describes how to use arbitrary strings and numbers in more advanced settings than just independent NPs (and whether that is a good idea to do).

Read more

tags: gf